Big O Notation
What is Big O Notation?
In programming we are interested in writing efficient code which will run as quickly as possible. Big O Notation is used to evaluate the complexity of an algorithm. Complexity means the use of time, memory and resources. It focuses on the number of inputs to the algorithm. All of these tend to increase as the amount of data input increases.
Big O Notation assumes worst case. (for example if you are searching for an item, it's the last one you check). However, some exam questions will ask you to indicate Big O for best, worst and average case.
When calculating Big O discard all but the most complex code. Below, the nested loops has the most complex code. The algorithm would be classed as having polynomial time complexity.

Big O is a tricky concept (which is why it's a popular programmer job interview question). Click here for a great explanation.
How does it work?
Big O compares complexity based upon the number of inputs. The complexity should focus on the code with the highest impact on performance and ignore everything else. In Big O the number of inputs is represented by n.
Steps to analyse an algorithm's complexity:
- Remove any code with a constant complexity (not affected by inputs)
- Calculate Big O.
- Focus on the most complex.
O(1) - Constant Time Complexity
O(1) performs at a constant rate. This means that the number of inputs does not effect complexity. In the code below the array could be 5 items or 1,000 items and it would still take the same amount of time to execute
int[] arr = [1, 2, 3, 4, 5];
Console.WriteLine(arr[0]);
Another example is using push() or pop() operations on a stack. Only the top item is accessed regardless of the size of the stack.
O(n) - Linear Time Complexity
O(n) increases at a linear rate. This means the complexity increases at the same rate as the data. 3 inputs will be 3 times slower than 1 input.
For example the following code loops through an array and prints each item:
foreach (string s in names)
{
Console.Writeline("Hello" + name);
Console.Writeline("how are you?");
}
One pass through an array will be O(n) as this will inspect each array element once.
O(log n) - Logarithmic Time Complexity
O(log(n)) increases at a logarithmic rate. The data set is halved each time it is run. On average Binary Search performs at Log(n). At each stage of the search we divide the array in half, so we successively reduce the size of the problem this way: n, n/2, n/4, n/8….
(For the mathematicians: in computer science just plain log means log2).
What is a logarithm?
Logarithms are used to solve for x when x is in the exponent. Look at this equation: (3^x== 9)
The question logarithms answer is: “What power do we raise 3 to to get 9?” The answer, of course, is 2! So log3(9) == 2.
When you say something grows exponentially, it’s being multiplied. When something grows logarithmically, it is being divided.
- Polynomial Time Complexity
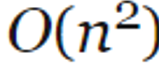
This indicates that the time it takes to run an algorithm grows as the square of n. Nested loops (loop within a loop) are great examples of polynomial time complexity. POLYNOMIALS
var n = int.Parse(Console.ReadLine());
for (var r = 1; r <= n; r++)
{
for (var c = 1; c <= n; c++)
{
Console.Write("*");
}
Console.WriteLine();
}
- Exponential Time Complexity
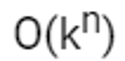
This is bad! This means that as n grows the complexity is going to increase significantly. This often makes an algorithm unusable.
What you Need to Know


Big O: Best to Worst Performing
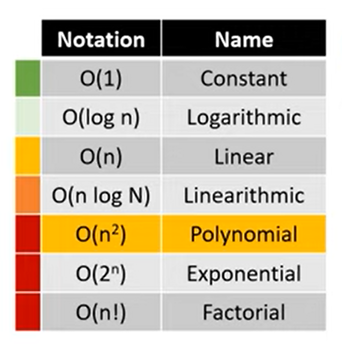
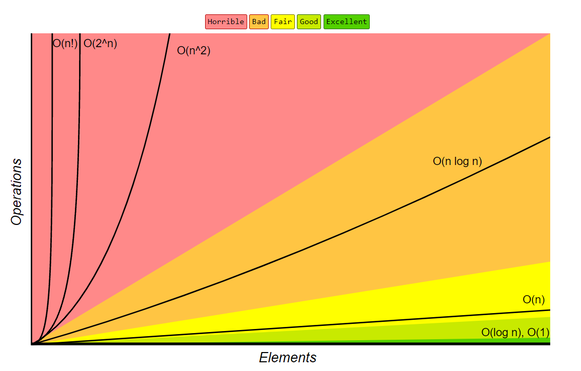
Big O for Searching Algorithms
Best case for searching algorithms is O(1). The size of the array doesn't matter because best case means that you you find the item straight away (regardless of the search algorithm used).


Big O Notation in Practice - Games Development
The following video discusses how to change code to better handle polynomial time complexity.