Advanced Data Structures
Hash Tables
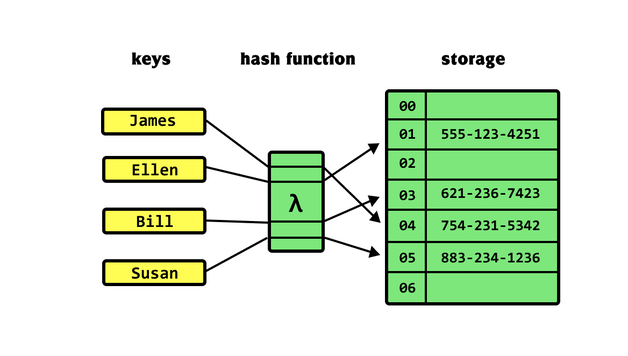
Hash tables are used where there is a large data set and items need to be found quickly. They are essentially arrays. But they store data into an array directly. They do this by running an algorithm on the data to be stored to calculate a hash value. This is the array index value. The data is then assigned to that hash table (the array) at that index.
Why use a hash table instead of an array?
Hash tables allow for efficient searching. You can search for a value by running the same algorithm on the data to find the hash value, that is the position in the hash table. Then you just retrieve the data at that position. This is obviously much faster than linear search and even binary search, Data in a hash table can be sorted or unsorted.
A Simple Example
Get an index position by:
- adding up the Ascii values of each letter in a word
- e.g. Apple adds up to 498.
- calculate the modulus using the size of the hash table on the total to find the remainder.
- .g. 498 % 10 = 8. Insert at position 8.
To find data in the hash table:
- perform steps 1 and 2 on the search value to find the index.
- check that index position in the array for the data.
Collisions and re-hashing
What if there is a collision (an item already at the position)? An alternative position must be found. This is called re-hashing. There are several ways to handle collisions.
The Overflow Table
Store the data in a separate array called the Overflow Table. Start at the beginning of the Overflow table and look for the next available space. When searching you can check the overflow table (linear search) if you can't find the search value in the hash table.
Linear Probing
Store the data in the hash table at the next available slot after the hash value position. When searching check the hash value. If the data isn't find perform a linear search starting at the hash value position.
This has the advantage of filling up one hash table. But this could also result in more collisions. It could also cause clustering where many positions are filled around common hash values.
Chaining
Use a 2D array and store collisions in the next column. Or use a linked list to store collisions in a new node.
Using a Linked List
You could use a linked list (see below) as an overflow table and add nodes for each new piece of data to be stored. To then search for a value in the linked list you would start at the first node and following the next pointers until either the value is found or you reach the end (if the data doesn't exist).
This is going to be a problem if the linked list grows as it will take longer to search. So using a linked list is considered to be the slower option.
What makes a good hashing algorithm?
Of course the best solution is to not have many collisions in the first place by creating a strong hashing algorithm which should:
- be calculated quickly.
- limit the number of collisions.
- use the smallest amount of memory possible.
Linked Lists
A Linked List is a linear data structure which consists of a group of nodes in a sequence. Each node contains two parts: the data and a pointer to the next item. Some also have a pointer back to the previous node which is useful if you want to search back and forth through the list.
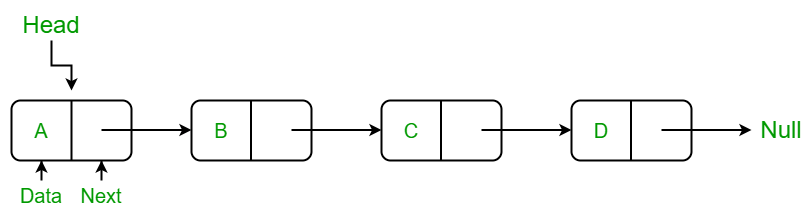
Traversing
To traverse (go through) a linked list start at the first node and follow the next pointers to move through each node until you get to the end where next will point to null.

To append an item to the end.
Traverse all the way to the end and then set the final node's next point to point to a newly created node.
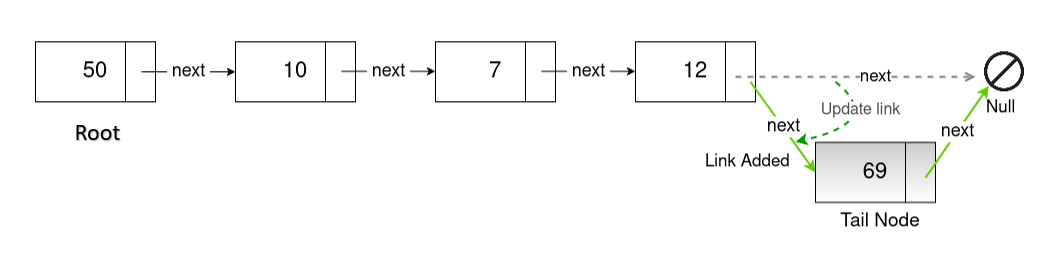
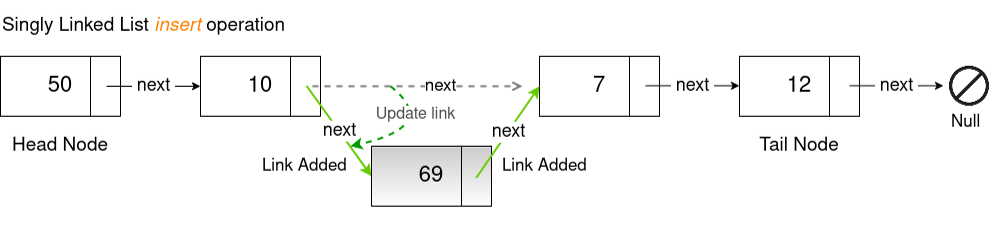
To insert a node at a particular position
Traverse through the nodes until you get to the position before where you want to insert. Set the new node's next pointer to the current node's next pointer. Then set the current node's next pointer to the new node.
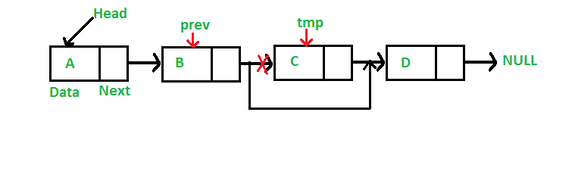
Deleting a Node
Deleting a node is a little trickier because you need to keep hold of the previous node as you traverse. Once you find the node to delete, you need to set the previous node's next pointer to the current node's next pointer. In some programming languages you should dispose of the deleted node to release its memory. C# does this for you.
Records
It's easy to store single bits of data into primitive data types such as variables. However, often these bits of data are related. Related data should group primitive data types together to create compound data types. One of example of a compound data type is a record. These are frequently used in databases but can also be created in code.
Records are like a light version of classes that only store member variables. So they have the benefit of being simple and low on memory. But they don't include any useful behaviour that you might program into a member method.

Tuples
A tuple is another compound data type. A tuple is a bit like a list in that it stores data together. However the data is immutable. This means that it can not be changed once the program is running. The key difference between tuples and lists is that while tuples are immutable objects, lists are mutable. Tuples are also more memory efficient than the lists.
 TUTORIALSTEACHER
DOTNET PERLS
PROGRAMIZ
TUTORIALSTEACHER
DOTNET PERLS
PROGRAMIZ
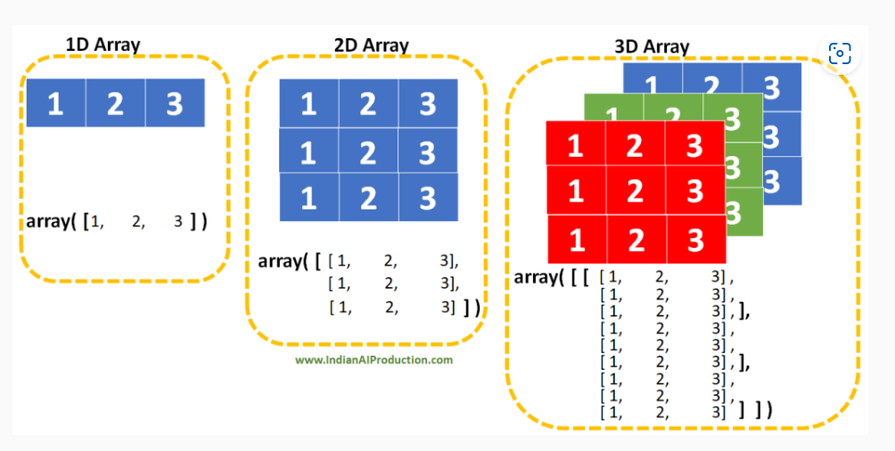
3D Arrays
At GCSE covers 1D to store one set of data and 2D arrays to store a table of data in rows and columns. 3D arrays go one step further in that it includes three dimensions which you can think of as rows, columns and blocks.
 ISAAC COMPUTING
TUTORIALSTEACHER
ISAAC COMPUTING
TUTORIALSTEACHER
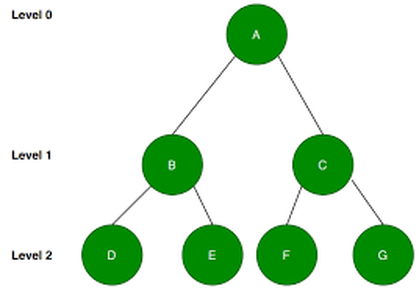
Graphs and Trees
Graphs and Trees are both dynamic (can grow and shrink) non-linear data structures which consists of nodes that are connected by edges.
Graphs
Graphs connect nodes (or vertices) together. The connecting line is called an edge. They are used to represent real life connected systems such as networks.
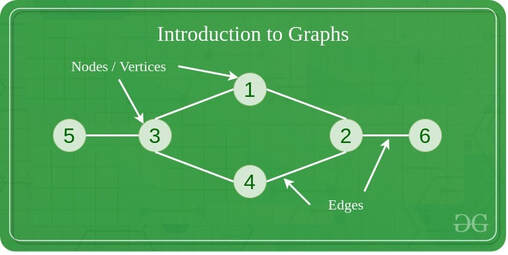
When traversing along edges graphs can be directed (one way) or undirected (two way). Graphs can also be weighted where each arc has a cost attached to it.
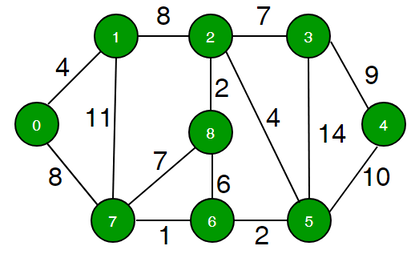
Graphs are commonly stored as objects. But you can also store them in an array (an adjacency matrix) where 1 or 0 is used to denote an edges between vertices
Uses of Graphs
Graphs can be used to represent such as road navigation systems, social network data, molecular structure representation.
Trees
The tree data structure is often used to organise and sort data e.g. file management. Tree represents the nodes connected by edges. A rooted tree is a tree with one node that has been designated as the root. Unlike real trees, when representing rooted trees in a diagram, the root is placed above the other nodes and the branches descend to the leaf nodes. A leaf node is the final node at the end of a branch.
You can traverse along a tree by starting at the root and following each each to each node until you reach the leaf node.
Uses for Trees
File or folder structures. The A* path algorithm. Any structure with parent and child nodes e.g. a corporate structures.

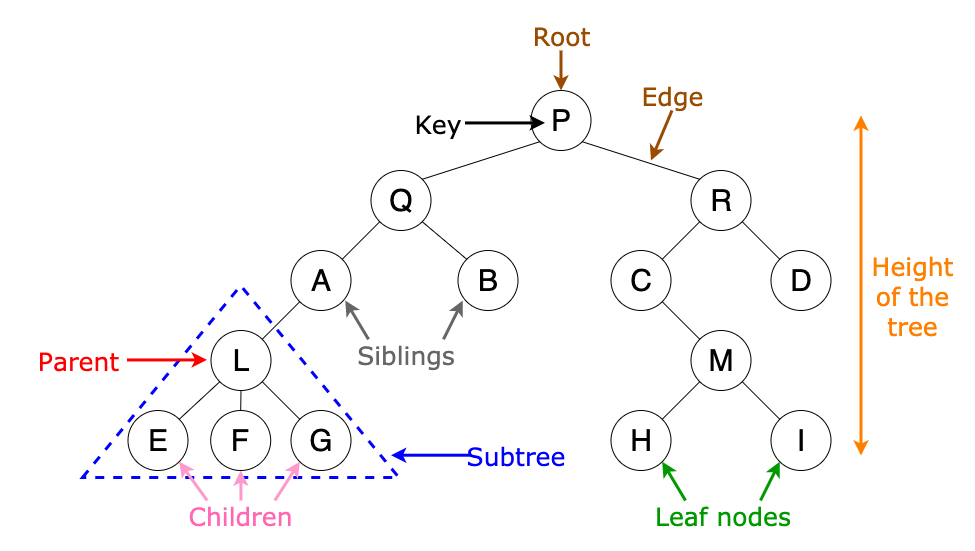
Binary Trees
Binary trees are a special type of tree as each node has at most two child nodes, often referred to as the left node and the right node.
Binary trees are used in database applications etc. to easily sort or search. This is easy as data can be easily stored in order.
Graphs and Trees - What's the difference?
Similarities:
- Are non-linear, unlike an array or list.
- Are dynamic, unlike an array. So they can grow or shrink in size.
- Have nodes.
- Have edges.
Differences:
- A tree is 1-directional whereas a graph is 2-directional.
- A tree has a root node whereas a graph does not necessarily have one.
- Tree will not have cycles whereas graphs can contain cycles.
- Tree are never weighted, graph edges can be weighted.
Graphs and Trees - Searching
Depth First searching involves visiting each vertex and exploring each branch as far as possible before backtracking. Whereas Breadth First searching involves starting at the root and visiting each neighbouring node before moving to the vertex at the next depth,
Depth First: PreOrder, InOrder and PostOrder
These are the three common ways to traverse a tree depth first.
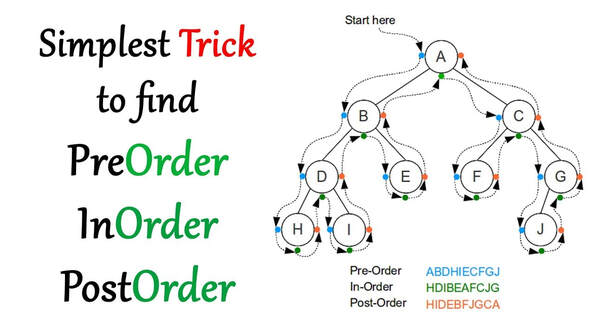
-
PreOrder: Root --> Left SubTree --> Right SubTree. Nodes are traversed in the order you pass them on the left. In other words as you come up to them the first time, hence the "pre".
-
InOrder: Left SubTree --> Root --> Right SubTree. Nodes are traversed in the order in which you pass under them.
-
PostOrder: Left SubTree --> Right SubTree --> Root. Nodes are traversed in the order you pass them on the right. That is, after you have visited them for the last time, hence "post".