Sorting Algorithms
It is common to need to sort an array of data (e.g. to put names in order, add scores to a leaderboard). There are several different pre-defined sorting algorithms you can use to sort your data:
GCSE
You must know how the following sorting algorithms work. You will likely be asked to create a trace table showing a short array changing for each iteration of the loop.
You will not be expected to write or understand the code for sorting algorithms.
- Bubble Sort
- Insertion Sort
- Merge Sort
A Level
You must know the following sorting algorithms including to write them in pseudocode.
- Bubble Sort
- Insertion Sort
- Merge Sort
- Quick Sort
Bubble Sort
Bubble sort is an algorithm that sorts a collection of data by ‘bubbling’ values to the end of the list over successive passes (loops through).
- On the first pass the highest value (or lowest, depending on the sort order) is moved to the top of the list.
- On the second pass, the second-highest item bubbles to the next-to-top place, the third-highest on the third pass, and so on, until it has produced a sorted list.
The algorithm is called bubble sort because the items are bubbled up the list one place at a time, which some people imagine as bubbles in a fizzy drink rising to the top.
Is Bubble Sort efficient?
Bubble sort can be fast if most items are in order. Otherwise it can be slow because it would involve a lot of swaps.
The Swap Algorithm
int temp = nums[p];
nums[p] = nums[p + 1];
nums[p + 1] = temp;
A swap involves the following three lines of code.
- Temporarily store the first list item (as the next step will overwrite it).
- Set the first item to the next item.
- Set the next item to the temporary stored item.
How do we know when the list is sorted?
If you pass through the whole list without having to swap, you know you are done. We use a boolean variable to check for this. Swap in the example below. Line 2 of the condition controlled loop is the same as saying While (Swaps == true).
PseudoCode for BubbleSort

BubbleSort in C#
bool swaps = true;
while (swaps) // same as (swaps == true)
{
swaps = false;
for (int p = 0; p < nums.Length - 2; p++) {
// selection...
if (nums[p] > nums[p + 1]) {
// swap...
int temp = nums[p];
nums[p] = nums[p + 1];
nums[p + 1] = temp;
// we had more swaps to perform...
swaps = true;
}
}
}
Bubble Sort in Folk Dancing!
Watch the following video to see folk dancers achieve a bubble sort.
Insertion sort
- In sertion sort works by building up a sorted list within the unsorted list.
- At the beginning you have an unsorted list. For insertion sort you start by considering the first item in the list as a sorted list. The rest is unsorted.
- You can take the item to the right from the sorted list and insert it into the correct position in your sorted list of one.
- Repeat the step above until you have a sorted list.
- As you build up a sorted list by inserting each item into the correct position in the increasingly sorted list on the left. Find out more here.
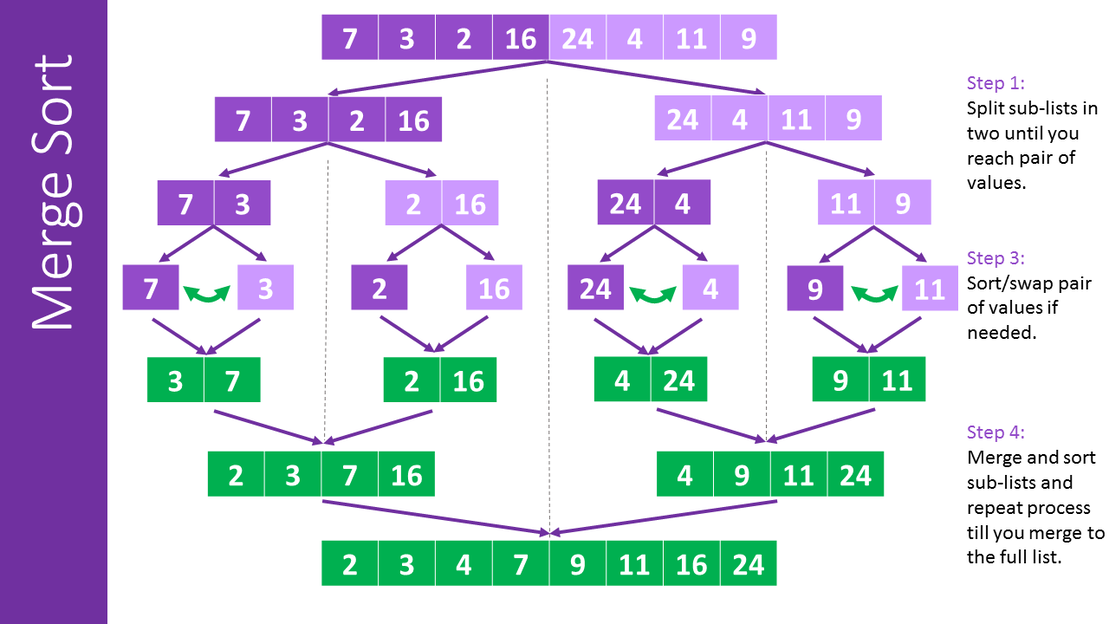
Merge Sort
Merge sort is fast because it has a divide and conquer approach. It works by repeatedly spitting an unsorted list into two halves until you are until you have individual elements and so can’t split any more. Then each “halve” is then merged back together in the correct order.
Here are the steps:
- The array is split into individual elements. Normally by halving the array continuously.
- Each individual item is merged back into a sorted list of 2.
- Each list of 2 is merged into a sorted list of 4.
- Each list of 4 is merged into a sorted list of 8.
- And so on until you have one list.
Note:
- When merging the halves back together. The lowest value is taken from the front of the list and placed into the new merge list.
- For example with the two halves below, Both halves would be checked for the first item. 1 is the lowest so it would be inserted. Then the first item in both halves would be checked again. 2 is the lowest so 2 would be inserted next.. and so on.
[1,3]and [2,4]
would merge to
[1,2,3,4]
This is faster than Bubble Sort if the list is large or very unordered. Remember swapping (used for Bubble Sort) involves three lines of code and one extra temporary local variable.
Find out more here.
ISAAC COMPUTING - INSERTION SORT
BBC Bitesize
Click here for an excellent explanation from BBC Bitesize.
A LEVEL ONLY
Quick Sort
Quick sort is, well, quick! It uses a divide and conquer approach. It uses a pivot value to which all other values are compared. Values lower than the pivot are moved before it. Values higher than the pivot are moved after it. It is similar to merge sort but takes up less memory as the sorting is done in place rather than in separate lists. Find out more here.
Quick sort is considered to be a "divide and conquer" algorithm because it splits the data into sub sets (using the pivot). It then sorts each sub set. The sub sets are then combined to provide a sorted list of elements.
Uses of Quick Sort
Quick sort is considered to be very fast and efficient, so it is used for large data sets and critical, real time programs such as medical life support, aircraft and defense systems.
Choosing the pivot value
It would make sense to choose the median value as the pivot. But with an unsorted list how do we know the median value? So any element can be chosen. It is common to choose the first element.
The Quick Sort Algorithm
Quick Sort can be written in many different but similar ways. There is always a pivot used to split the data set (e.g. array) in two. There are always two pointers for the beginning and end of the data set. The pointers and data can both swap. One or both of the pointers can move towards the other.
Quick Sort Steps
The Algorithm - using Recursion
public static int[] QuickSort(int[] items, int start, int end)
{
// Base case for recursion:
// The recursion will stop when the partition contains a single item
if (start >= end) {
return new int[0];
}
// Otherwise recursively call the function
else
{
int pivotValue = items[start]; // Set to first item in the partition
int lowMark = start + 1; // Set to second position in the partition
int highMark = end; // Set to last position in the partition
int temp;
bool finished = false;
// Repeat until low and high values have been swapped as needed
while (finished == false) {
// Move the left pivot
while (lowMark <= highMark && items[lowMark] <= pivotValue) {
lowMark = lowMark + 1; // Increment lowMark
}
// Move the right pivot
while (items[highMark] >= pivotValue && highMark >= lowMark) {
highMark = highMark - 1; // Decrement highMark
}
// Check that the low mark doesn't overlap with the high mark
if (lowMark < highMark) {
// Swap the values at lowMark and highMark
temp = items[lowMark];
items[lowMark] = items[highMark];
items[highMark] = temp;
}
// Otherwise end the loop
else {
finished = true;
}
}
// Swap the pivot value and the value at highMark
temp = items[start];
items[start] = items[highMark];
items[highMark] = temp;
// Recursive call on the left partition
int[] Left = QuickSort(items, start, highMark);
// Recursive call on the right partition
int[] Right = QuickSort(items, highMark + 1, end);
// items = Left + Right;
return items;
}
}
Walkthrough from 3:40.