Binary
Binary... what is it and why does it matter?

Binary is a number system. But instead of having ten numbers to choose from we only have two. I’m sure you’re pretty good at counting by now, so why do we need another number system? What’s more why do we need binary when it limits us to only two numbers 0 and 1 to represent any number?
Here’s Sophie, She’s considered to be so humanlike that she’s actual a citizen of Saudi Arabia!
However everything Sophie hears, says, does, understands is transalated down to 1s and 0s which are passed to her transistors.
Binary is all that your computer understands,
Watch this Crash Course video to find out more about binary and how transistors (those little black and green items below) work.
You can find out even more by watching this video when you're ready.
Understand... a bit
Now that you understand that computers use transistors which are either on or off to represent 1 or 0. You need to understand a bit. A bit stores either 1 or 0 in the computer's memory. This could be your desktop computer memory or your USB drive, or any other device which has memory... even an apple watch.
How does binary work?
We need to understand how to convert between decimal (our number system) and binary. Watch the video below and read on to find out more,
How do we normally count?
Our number system is called decimal. Decimal is base 10, which means that we use ten different numbers from 0 to 9. For anything bigger than 9 we repeat the numbers.
Look at the power line (top line). Position is important.
- The first position being units
- The next number on the left of units is the tens
- The next number on the left of tens is the hundreds
...and we keep going, that the power line multiplies by 10 every time add a number to the left.
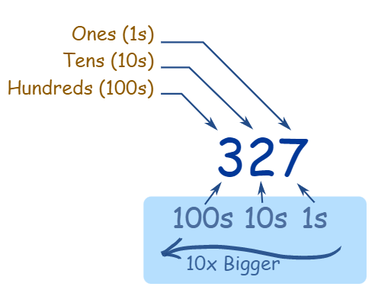

Did you know?
In maths we can represent each number to the power of 1, 2, 3. Above you can see this all the way to billions.
Binary Numbers
Binaryis base 2, which means that we only use two different numbers 0 and 1 to represent numbers. So for any number bigger than one, we repeat the numbers.
So how do we work out how to make up a binary number? Let’s try the binary bank challenge.
Converting Decimal to Binary with the Binary Bank example
Let’s start simple with The Bank of Binary. This imaginary bank has only four coins. Check the image below. How would you make the number 3?

You’d use the coins with the values 2 and 1. How about 10? Remember that you can only use each coin once.
You’d use the coins 8 and 2. In this way we can make up any number up to 15.
Below we can see the coins laid out in order from biggest to smallest.

The bottom row shows which coins have been selected:
- The number 1 means use the coin. The number zero means don’t use it.
- Here we can see that the coins with values 1, 2 and 8 have been selected.
- These coins add up to 11.
- To work out the binary we just write out the bottom line.
- So the binary for 11 is 1011.
Converting Binary to Decimal
Look at the coins above laid out in order. Can you work out the decimal for the binary number 1001?
Let’s see the number written out..

When we write in the digits we see that this means we have 1 for the coins: 8 and 1, totaling 9. Here’s your next challenge... try to work out the decimal for 0111.

This would mean we have one of each of the following coins: 4, 2 and 1. The three coins add up to 7.
Working out bigger numbers
So binary is easy to work out by writing out the binary number line. From right to left that’s 1, 2, 4, 8.
What if we want to work out a number greater than 15 in binary? We would have to extend the power line, which is the top line giving the value of each coin. What do you think comes after 8? Can you see a pattern? I’ll give you a clue binary is base 2. This means we multiply by 2 to get each number. 1 then 2 then 4 then 8 then... our new number 16. We keep multiplying until we have the full 8 bit binary number line. Check the numbers in grey below.
Binary... in bits!
So if we have a binary number like 1001, how many bits will it take up in memory? The answer is 4. One for each 1 or 0. 4 bits is called a nibble (see right for more memory keywords). Memory chunks are normally divisible by 8.
Ascii: Representing letters
So now we know how to convert between our number system (decimal) and binary so that a computer can understand. But what about letters, punctuation and those emojis we all love? Ascii was invented as is system where each of those alphanumeric (letters etc.) are represented by a number. That number can then be turned into binary.. because we know that's all computers understand! In ASCII is each letter is assigned a number between 0 and 127. Upper and lower case character are assigned different numbers. For example, the character A is assigned the decimal number 65, a is assigned decimal 97. Here is the Ascii table. Can you work out the numbers for the word "Hello" ?
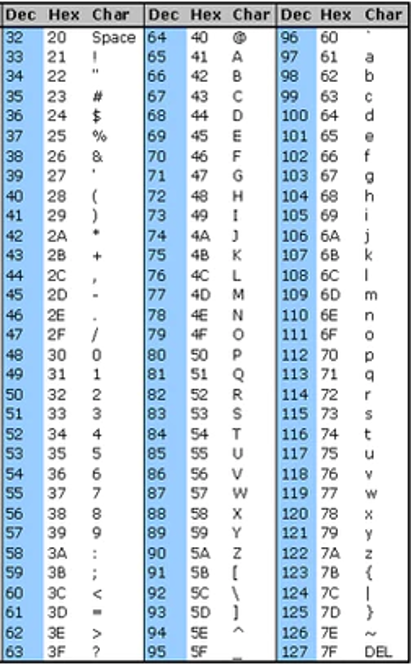
You should have the following:
- H is 72
- e is 101
- l is 108
- l is 108
- o is 111
Now let’s convert each of those numbers to binary:
- 72 is
01001000 - 101 is
01100101 - 108 is
01101100 - 108 is
01101100 - 111 is
01101111
So the binary for Hello is:
01001000 01100101 01101100 01101100 01101111
Want to know more about binary?
Extended Ascii
Ascii doesn’t allow us to represent everything, just letters, punctuation and most things on a standard keyboard. However, computers need to work with more than that these days, such as letters with accents used in European languages. For this we need extended Ascii.
Unicode

The Ascii table was created in 1963. Back then programmers were not always thinking globally. Unicode provides a unique way to define every character in every spoken language of the world by assigning it a unique number. You can even represent emojis!