Advanced Binary
What is Binary and Why do We Need it?

Computers use binary for calculations and logic. Two states are easy to build into electronic circuits. Inputs are either 0 or 1.
Binary is a number system which only uses two numbers: 0 and 1. If you are new to binary check the this web page for an introduction. Programs are compiled into binary to be run. When run billions of transistors are turned on (1) and off (0).
Understanding Binary Numbers
Our normal number system, denary, has ten numbers from 0 to 9. Thus to represent numbers greater than 9 multiple numbers are required. Binary only has two numbers, thus to represent numbers greater than 2, multiple numbers are required.
Denary is based 10. The number line is multiplied by 10. Binary is based 2 so we multiply the number line by 2. See the example below for the number 93. Each number takes up one bit of data.
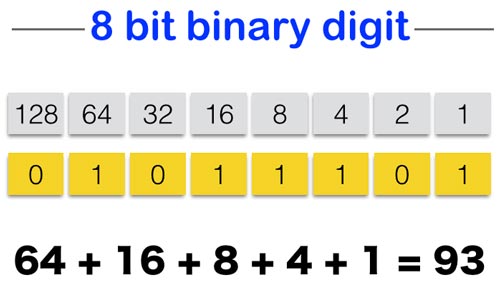
NOTE:
In exam questions unsigned numbers are positive numbers i.e. no negative sign.
Neat Tricks: Converting from Binary to Hexadecimal
This is easier than you might anticipate! Just split the binary into groups of 4 binary digits and convert each separately. Then put the result together.

Converting Denary to Hexadecimal... via Binary
As the wise Louis once said (don't put that on your exam), an easy way to convert from decimal to Hexadecimal is to first convert to binary and then Hex. Here is an example with the number 166:

Binary Arithmetic
Binary addition is similar to denary addition. We add and carry the numbers that don't fit. But what happens if there is no room to store the carried one?
We get an overflow error. In other words the resulting number is too big to be stored in the available memory.
Note: you must show the carry on your exam answers.
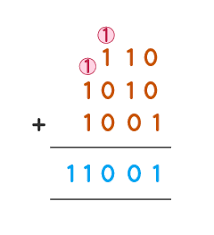
Representing Negative Numbers
You only have a choice of 1 or 0. You don't have a - sign. So how do you represent negative numbers? There are two methods: Sign and Magnitude and Two's Complement.
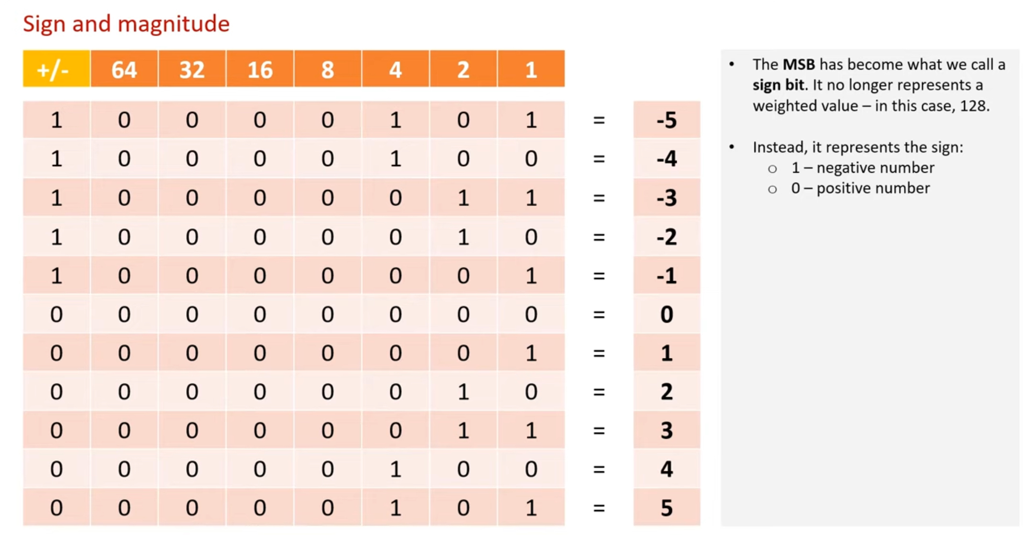
Method 1. Sign and Magnitude
Use Most Significant Bit (the left most bit) to indicative positive or negative:
- Set to 1 means that the number is negative.
- Set to 0 means that the number is positive.
So the number 10000011 is actually -3.
Sign and Magnitude is rarely used!
This system is used in ordinary arithmetic but is awkward when employed in computer arithmetic because one of the bit patterns is wasted as there are 2 different representations for 0 i.e., + 0 and – 0 having different representation in the signed-magnitude system but the value is same.
It is not shown here. But the number 10000000 is also zero!
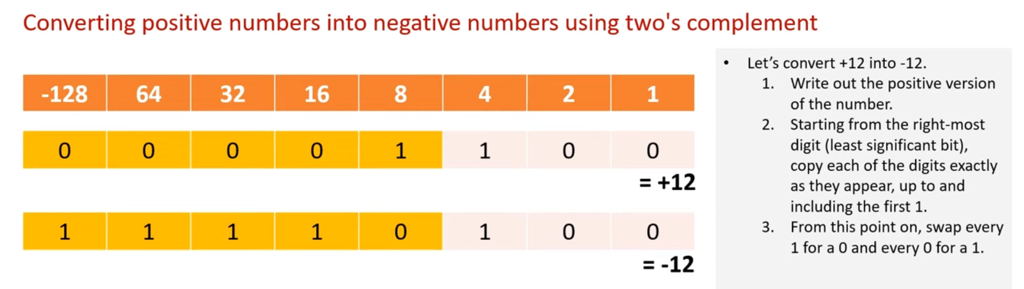
Method 2: Two's Complement
In two’s complement the Most Significant Bit is set to the largest negative number which is -128. The other bits are used to add to the left most bit to achieve the desired negative number.
There is a neat trick...
- Start with the positive version of the desired negative number.
- Copy down the values up to and including the first 1.
- Then flip the remaining bits.
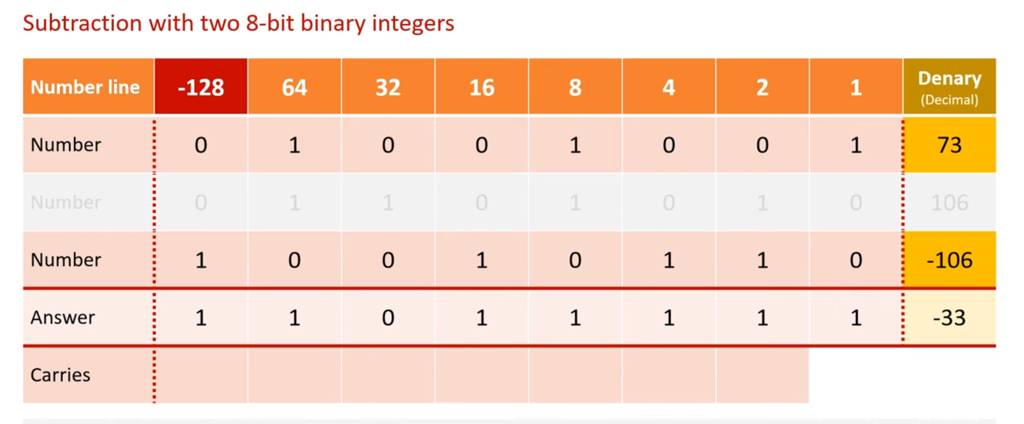
Binary Subtraction
The easiest way is to turn the number to be subtracted into the negative version of the number..
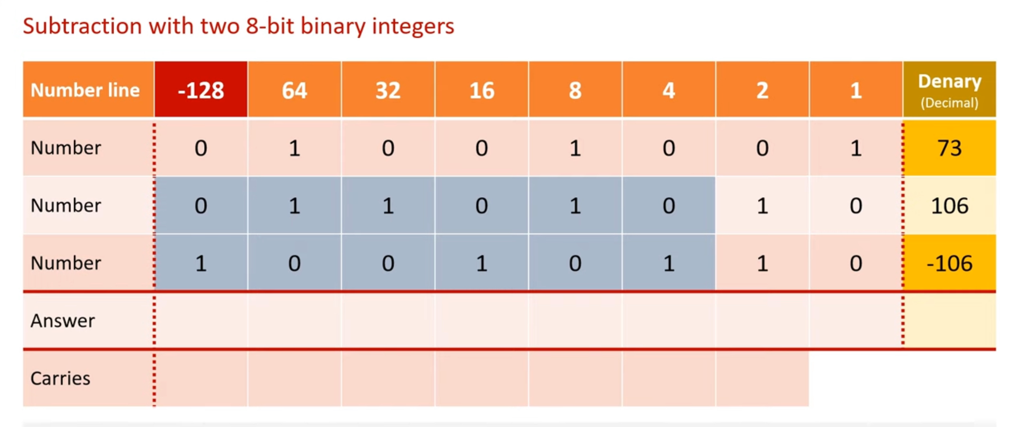
...and then add the numbers...
Floating Point Numbers in Binary
Fixed Point Binary
To represent fractional numbers we can add a Binary Point. The numbers to its right represent fractions. This means that the range of numbers will be more limited. This also limits precision as you can only represent some fractions. You couldn’t represent a third. Fixed Point Binary the Binary Point is set in a fixed position. This is easy.. but limits all numbers to the same level of precision and the same range of values. What if you need some numbers to have high precision and others to be larger numbers with less precision?
Floating Point Binary
We can change where the binary point is placed depending on whether we can to increase the size or the number and the precision.
But we would need to know where the Binary Point is!
We can split the number into the Mantissa and the Exponent. How many bits are used for each will always be stated.
- Start with the Binary Point after the Most Significant Bit.
- Convert the exponent.
- Move the Binary Point three places to the right.
- Adjust the number line.
Note: If the exponent is negative the move to the left.
Normalisation
Floating Point Binary just described can come up with the same number several ways. To ensure consistency we normalise the numbers.
Normalised positive numbers start with 01.
Normalised negative numbers start with 10.
Move the Binary Point so that it sits between the 0 and the 1. The exponent should be set to the number of spaces moved.
Normalising negative numbers
- Find the negative as shown above using Two’s Compliment.
- Move the Binary Point so that it sits between the first 1 and 0 (since all negative numbers start with 10). As before the exponent should be set to the number of spaces moved.
Will this always work?
You can lose some precision using this process if there is insufficient space in the Mantissa.
Adding up Floating Point numbers
Work out where the Binary Point should be based on the exponent.
Line up the Binary Points. Then add as normal.
Binary Shifts to Multiply or Divide.
Take a binary number and shift each digit to the left to multiply by 2. Note you’d lose the left most bit. Shifting right divides by 2. This only works with positive numbers. It wouldn’t work with negative numbers as the Most Significant Bit would be lost! (It will work with an arithmetic right shift (add the previous MSB value to the MSB) but this is not on your exam).
Bitwise Operations and Masks
Masking uses the logical operators described above to toggle/flip or extract a sequence of bits.
See the example below using an AND mask. The bitwise operators have the following effects.


XOR
Use XOR to flip the bits.

Why do this?
One example is in networks where the mask 255.255.255.0 can be used to isolate the network location.